Advent of Code Day 6-Maps, Sets and Optimizations
Today’s Advent of Code Puzzle had us “redistributing” data inside an array. We needed to perform a series of redistributions and stop when we detected that the array has returned to a state we’d seen before (indicating an infinite loop in the redistribution algorithm).
Part 1 – Using Sets
I needed a couple of helper methods to solve this. First, findMaxIndex to find the index of the maximum item in an array:
function findMaxIndex(arr) {
let maxIndex = 0;
for(let n = 1; n < arr.length; n++) {
if (arr[n] > arr[maxIndex]) maxIndex = n;
}
return maxIndex;
}
Next, the redistribute function which takes an array and returns a “redistributed” array. You’ll notice that this isn’t a pure function – I simply mutate the input array and return it (we’ll come back to that later).
function redistribute(banks) {
const maxIndex = findMaxIndex(banks);
// redistribute
let amount = banks[maxIndex];
banks[maxIndex] = 0;
for(let n = maxIndex + 1; amount > 0; n++, amount--) {
banks[n % banks.length] += 1;
}
return banks;
}
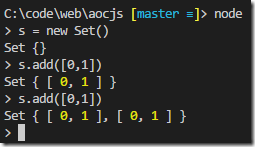
And finally we need to keep calling redistribute until we get a duplicate. But how can we compare arrays? The ES6 Set class sadly doesn’t see two identical arrays as being the same object. We can test this with the handy node REPL and see we can add the “same” array of integers twice.
But there’s a quick and easy hack we can use to get round this. Just call toString on the array and put the string representation in the Set.
Here’s a quick and dirty implementation for counting redistributions using a Set of strings:
function countRedistributions(state) {
let seenStates = new Set();
seenStates.add(state.toString());
let redistributions = 0;
do {
state = redistribute(state);
seenStates.add(state.toString());
} while(seenStates.size > redistributions++);
return redistributions - 1;
}
That enables us to solve part 1:
function solve(input, part) {
if (part === 1) {
const banks = input[0].split('\t').map(Number);
return countRedistributions(banks);
}
}
Part 2 – Upgrading to Maps
For part 2, we needed to remember not just previous states, but how many redistributions there were to get into that state. We can do this by upgrading from Set to Map keyed on the string representation of the array, and with the redistribution count as the value. The updated countRedistributions now returns not only the number of redistributions, but also the size of the “loop”:
function countRedistributions(state) {
let seenStates = new Map();
seenStates.set(state.toString(), 0);
let redistributions = 0;
for(;;) {
state = redistribute(state);
let key = state.toString();
redistributions++;
if(seenStates.has(key)) break;
seenStates.set(key, redistributions);
}
return { redistributions: redistributions, loopSize: redistributions - seenStates.get(state.toString()) };
}
We can now solve both parts of the puzzle with this one function:
function solve(input, part) {
const banks = input[0].split('\t').map(Number);
if (part === 1) {
return countRedistributions(banks).redistributions;
}
else {
return countRedistributions(banks).loopSize;
}
}
Optimizations
Yesterday I explained why I hadn’t gone for immutable arrays and there was some good pushback from Mikhail in the comments.
There are (at least) two ways my solution could be improved. First, the redistribute method is inefficient if a large number needs to be redistributed. We should only need to modify each entry in the array once, rather than looping round incrementing by one.
Here’s a faster redistribute function that updates each slot a maximum of once:
function redistribute(banks) {
const maxIndex = findMaxIndex(banks);
const amount = banks[maxIndex];
const addToEach = Math.floor(amount/banks.length);
const extras = amount % banks.length;
banks[maxIndex] = 0;
for(let n = 0; n < banks.length; n++) {
banks[(n + maxIndex + 1) % banks.length] += addToEach + ((n < extras) ? 1: 0);
}
return banks;
}
But this function is still ugly as we mutate the input banks array. We can quite easily make this into a pure function by taking a copy of banks up front:
function redistribute(banks) {
const maxIndex = findMaxIndex(banks);
banks = Array.from(banks); // to make this function pure
const amount = banks[maxIndex];
const addToEach = Math.floor(amount/banks.length);
const extras = amount % banks.length;
banks[maxIndex] = 0;
for(let n = 0; n < banks.length; n++) {
banks[(n + maxIndex + 1) % banks.length] += addToEach + ((n < extras) ? 1: 0);
}
return banks;
}
There are of course other ways of doing this, but now we’re returning a new array and leaving the one we were passed in unchanged.
What’s the cost of doing this? Well, I added a timing function to my puzzle solver framework, using process.hrtime which is the recommended way to time functions in node. Here’s my timing helper that returns the function result and the duration in milliseconds:
const timed = fn => {
const start = process.hrtime();
const output = fn();
const [secs,nanosecs] = process.hrtime(start);
const duration = secs*1000 + Math.floor(nanosecs/1000000);
return [output, duration];
}
This revealed that my first optimization didn’t make a huge difference on my input. And if we look at the numbers I had we can see why:
11 11 13 7 0 15 5 5 4 4 1 1 7 1 15 11
We rarely had to loop round all banks more than once as part of redistribution. Had these numbers been in the thousands, the optimization would have made a big difference.
And what about making redistribute pure by returning a new array? Well, that roughly doubled the time this function took to run (although the times were very small in the first place). Is that a price worth paying? Well for a simple puzzle like this it hardly matters either way. Immutability can bring a small performance penalty as in this example, but provides many benefits in terms of maintainability, testability and thread safety. And so even though I didn’t use it today or yesterday, I remain a big proponent of making your data structures immutable and your functions pure wherever possible.
 A place for me to share what I'm learning: Azure, .NET, Docker, audio, microservices, and more...
A place for me to share what I'm learning: Azure, .NET, Docker, audio, microservices, and more...