Advent of Code Day 15–Count Zip Take
A couple of days ago I mentioned that my utils library is slowly growing with LINQ-like methods as I’ve worked through solving the daily Advent of Code challenges this year. For today’s puzzle, I needed to create a new zip method, as well as use count and take.
The puzzle required us to generate a sequence of numbers, and to do so I created an ES6 generator function capable of generating the sequences we needed for both parts of the puzzle:
function *generator(seed,factor,test) {
let cur = seed;
for(;;) {
cur = (cur*factor)%2147483647
if (!test || test(cur)) yield cur;
}
}
This method generates an unending sequence, but we only needed to take a certain number of elements from the sequence (40 million for part 1, 5 million for part 2). So I need a take method that takes the first n elements from an iterable sequence. Here’s my implementation:
function *take(seq, count) {
let n = 0;
for(let el of seq) {
if (++n > count) return;
yield el;
}
}
Next, we were comparing elements in two sequences, and that’s where a zip method comes in handy. My zip method iterates through both sequences, yielding a two element array containing the pair of elements at the same position. It exits when either sequence ends.
function *zip(seq1,seq2) {
let it1 = seq1[Symbol.iterator]()
let it2 = seq2[Symbol.iterator]()
for(;;) {
let el1 = it1.next()
if(el1.done) return;
let el2 = it2.next()
if(el2.done) return;
yield [el1.value,el2.value]
}
}
And finally we needed to count how many elements in the zipped sequence matched a certain condition. I could do this by filtering my sequence with my where utility method and then passing it into my count method. But I decided to upgrade my count method to take an optional predicate to count all elements that match a certain condition:
function count(seq, predicate) {
let n = 0;
for(let el of seq) {
if (!predicate || predicate(el)) n++
}
return n;
}
With these very generic and reusable utility methods at my disposal, solving the challenge becomes very easy. I can combine them to count all the elements in the pair of sequences that match according to a specific rule:
function countMatch(seq1,seq2,n) {
const comp = ([a,b]) => (a&0xFFFF) === (b&0xFFFF); // brackets are needed!
return count(take(zip(seq1,seq2),n),comp)
}
One gotcha I ran into was the operator precedence of my comparison. The equality comparison clearly has higher precedence than the bitwise AND operator which was not what I was expecting:
All that remained was to parse my input and then use my generator and countMatch functions to solve both parts of today’s puzzle:
function solve(input, part) {
const parse = s => Number(/\d+/.exec(s)[0])
let genAStart = parse(input[0])
let genBStart = parse(input[1])
const aFactor = 16807, bFactor = 48271
if (part === 1)
return countMatch(generator(genAStart,aFactor),
generator(genBStart,bFactor), 40000000);
else
return countMatch(generator(genAStart,aFactor,n=>(n%4)===0),
generator(genBStart,bFactor,n=>(n%8)===0), 5000000);
}
As my utils library is slowly growing, I’ve started to break out the Jasmine tests for each utility out into their own “Spec”. It’s important to keep this utility code well covered by tests as these methods are being relied on in more and more places, and are slowly picking up new capabilities, such as the optional predicate for the count function. A good suite of unit tests protects against regressions and also is invaluable when attempting performance optimizations. Maybe I’ll see if I can turn my utils library into an npm package once I’m done.
 A place for me to share what I'm learning: Azure, .NET, Docker, audio, microservices, and more...
A place for me to share what I'm learning: Azure, .NET, Docker, audio, microservices, and more... 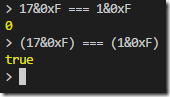
Comments
How was the performance of those solutions?
Mikhail ShilkovI solve all the challenges in scala fiddle site, which compiles it to javascript and executes right in browser. But today this schema proved to be quite slow...
it was slowest so far, about 8 seconds. It can be made much faster by not taking a functional approach and just doing the whole thing in a single loop. But I was happy to use this opportunity to create a few more reusable functions.
Mark Heath